The Inexperienced Coder: A Walkthrough of the Coding Experience

August 9, 2020CS Problemspinkpurplepineapples

I have a stack of magic the gathering cards, and wanted to track the price of my cards over time. I wanted to automate this process, and thought it would be interesting to talk about the entire process as an inexperienced coder.

Some caveats here:
I have a CS degree, but my expertise lean much more towards the theory side of things. I have a decent amount of experience in C++, with most of it being in competitive programming. I have basically zero software engineering experience and nothing I build here is going to display good software engineering practices.

The primary goal here is to illustrate the coding learning process, shed some insights, and hopefully make it less intimidating for newer coders.

I have my magic the gathering collection on deckbox.org, which has an option allowing for the collection of cards and prices to be downloaded as a csv file.

Hovering over the Export button in the top right shows a dropdown option “Export to CSV”, which creates a pop-up. The pop-up has another dropdown, where the price can be selected to be included in the downloaded csv.

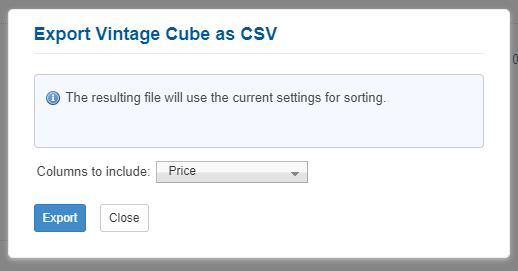
export csv export csv popup

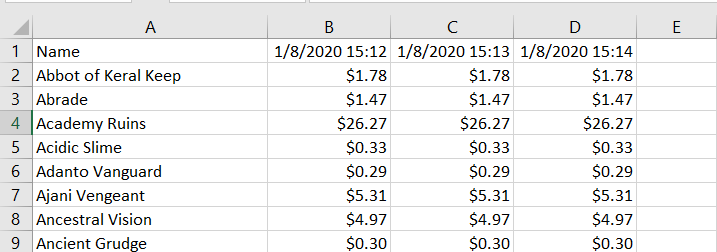
This generates a csv file that looks like this:

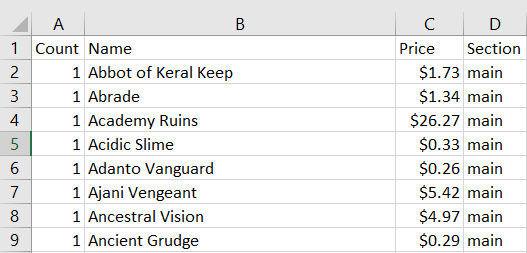
csv generated file

The goal is to write a script that queries the website daily for this csv file, and appends this set of prices to an existing csv file, along with a timestamp as a header:

csv end goal

I decided to use python, since python is really user friendly for projects like these. I happen to have very little experience with python, with maybe a few hundred lines of code written.

Since I know nothing about accessing the web with code, the first thing I do is google:

python interact with website

Clicking through a few links, I find this:

finding selenium
It seemed like there were a few options. Python has inbuilt functions for accessing and reading the text from websites, and several libraries exist that allow you to send HTML GET/POST requests. However, I don’t know much about HTML requests, especially not when it comes to their structure or formulation. I wasn’t sure if I would be able to easily input “Price” into the dropdown box through HTML POST requests.

Selenium seemed like a decent option, since it simulated the browser and let you click around and interact with the web objects, so that was what I decided to use. I already had python 3 installed through Anaconda, with the Spyder integrated development environment (IDE), so the first step was to install Selenium.

Setting Up Selenium

I start by googling:

python selenium

And click on the installation link. This brings us to the documentations page for Selenium, which has a very helpful installation guide:

installing selenium

As instructed, I run pip install Selenium on my Anaconda prompt, and download the Chromium driver, since I use Chrome.

To test to see if everything works fine, I click on the getting started page on the Selenium documentation page, and run their sample code: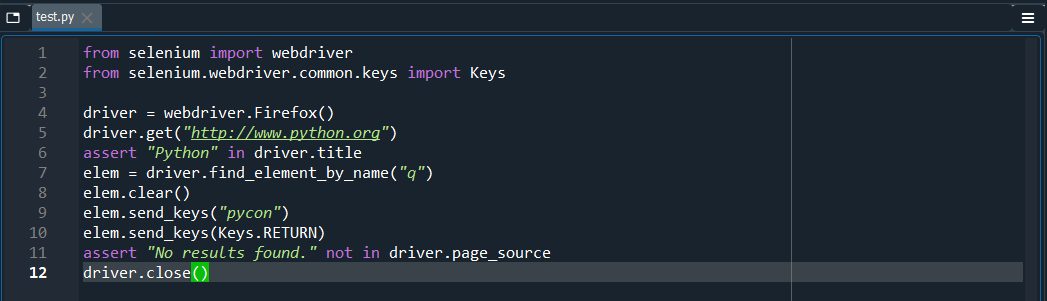

selenium test code

This gives me my first error:

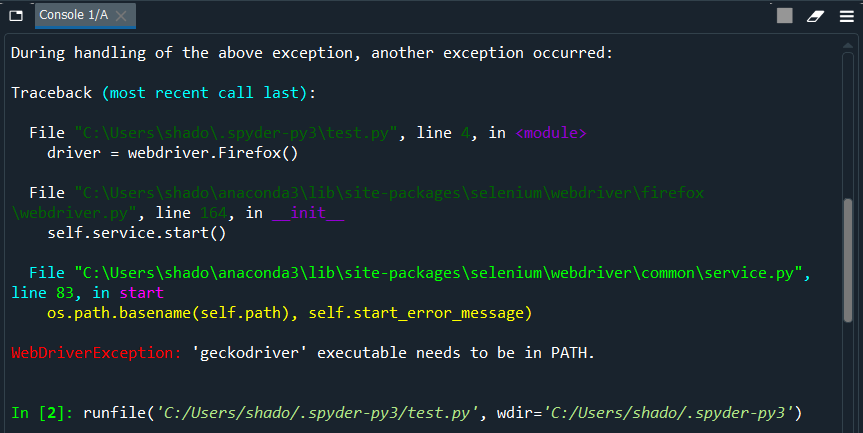
geckodriver error

A quick google reveals that geckodriver is the Firefox driver. Taking a look back at the default code, we see that it calls webdriver.Firefox() instead of the Chrome equivalent.

A quick check back on the documentation shows that the correct function call for Chrome is webdriver.Chrome()

accessing chrome

Editing my code and rerunning it gives a new error:

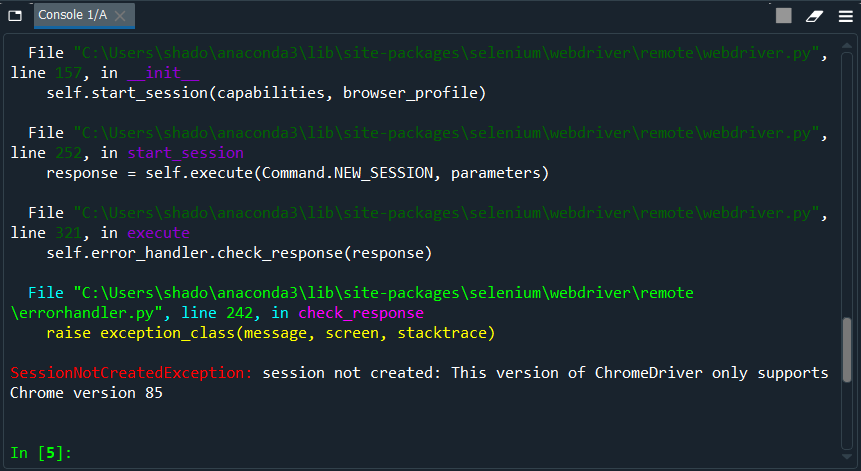
wrong chromium version

Googling this new error brings us to the following stack overflow thread:

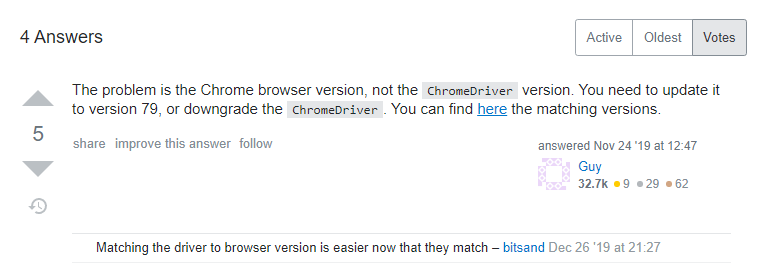
chromium version answer

Checking the downloaded versions, I see that I have Chrome version 84 installed, but Chromium version 85 installed. Reinstalling Chromium version 84, and rerunning our program gives us our first taste of success:

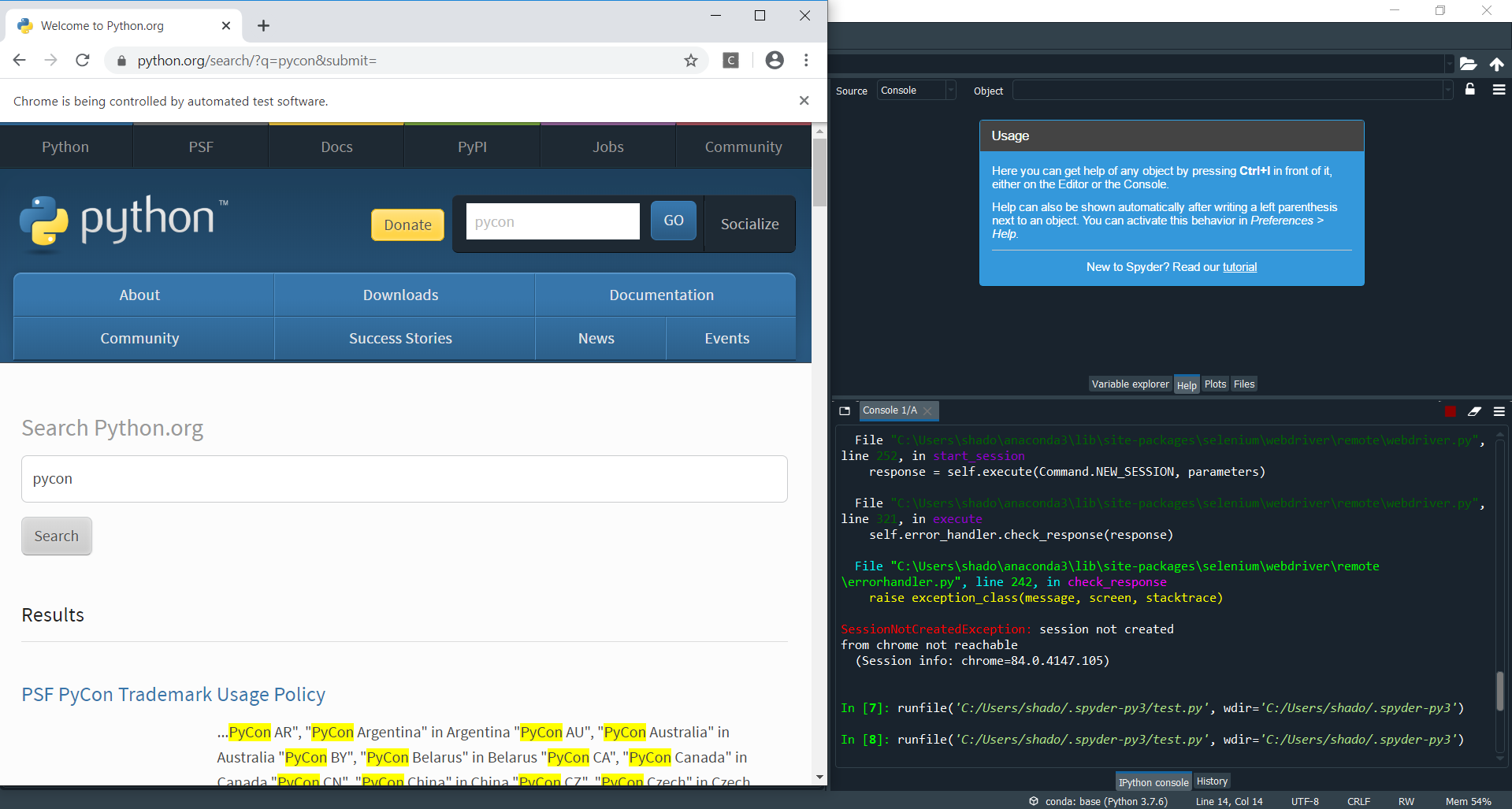
website loaded

The python.org page loads! Now we know that our installation is working.

Downloading the Data

Now that we have Selenium installed and working, we need to figure out how to use it to access the site. I would usually google “Selenium tutorial” at this point, and look for an easy to understand guide with some code, but in this case, Selenium has a great detailed guide in their documentation site, so I’ll be using that instead. Although sometimes technical and hard to parse, these documentation sites are usually the best place to get detailed information about what the available functions are, and the syntax for these functions.

We take a look at the example provided by Selenium:

selenium test code

And their explanation of the example available here:

understanding selenium

I also googled “selenium python web interaction”, and found this, a very useful walkthrough of Selenium, and how to use it. He included some code:

selenium code

And a brief description of how Selenium worked:

selenium how to navigate

Both these resources tell us the same thing, that the code to begin with is:

start code

It also tells us how Selenium works. We have to use the functions Selenium provides to select an object, to then be able to click on it. Let’s take a look at how the guy does it:

selenium tag lookup steps

Let’s try the same thing! Let’s inspect the element and see what tags we get:

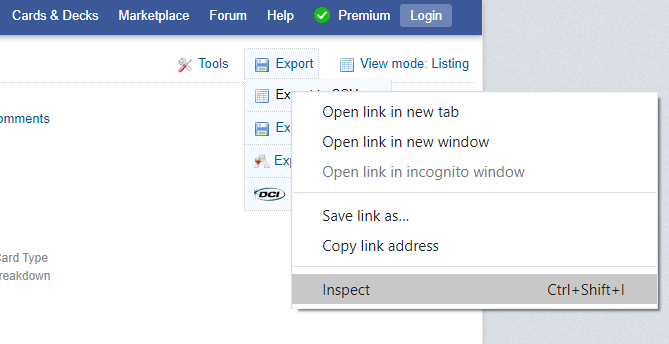
Unfortunately, it doesn’t seem like this HTML has an id tag. How else can we select this element? Going back to the documentation, we see:

ways to locate elements

Since id and name don’t work, lets try searching for it by xpath. A quick google of “finding xpath in chrome” gives this stackoverflow thread:

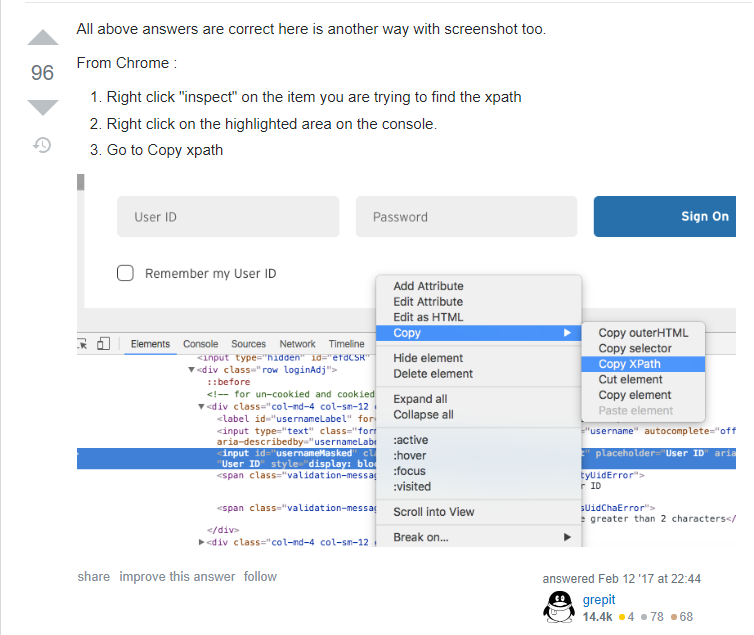
finding xpath

Repeating the same steps gives us the xpath: “/html/body/div[1]/div[2]/table/tbody/tr/td[2]/div[1]/ul/li[2]/ul/li[1]/a”

We want to click on this button to get our popup, so lets look for the click command in Selenium. A quick check on both our Selenium documentation and our walkthrough shows us that the command is just .click():

Adding this to our code gives:

click code

But this gives us another error message:

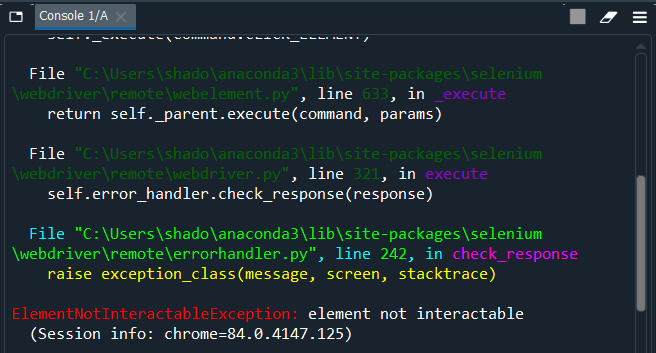
element not interactable

A quick google of “selenium element not interactable” gives us several stackoverflow threads about this error.

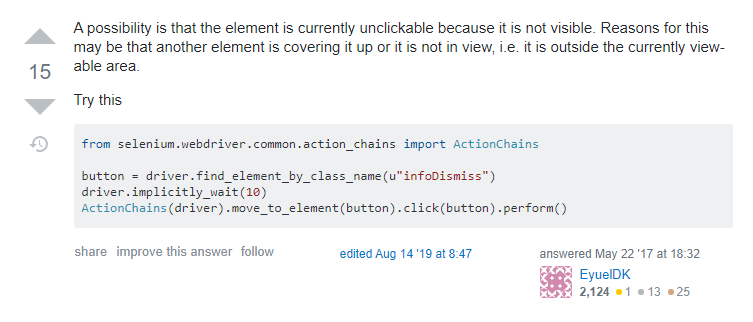
not visible answer

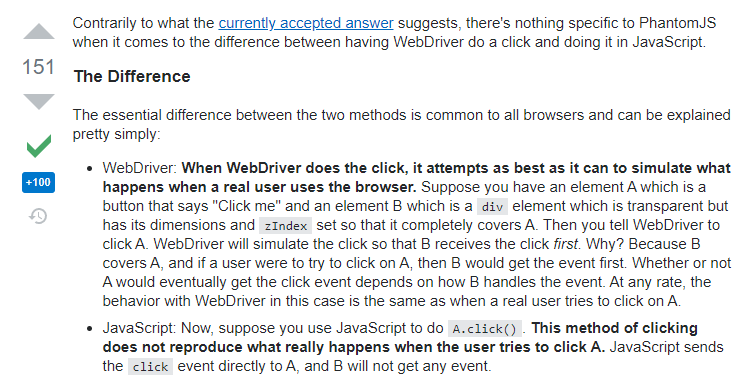
difference between javascript and selenium

So here we learn something about how Selenium works. Selenium simulates a browser, and can only access elements that can be seen. To access the “Export as CSV” button, we first had to click on the “Export” button. Since we had not yet clicked on the “Export” button, the “Export as CSV” button was not visible, so we could not interact with it, giving us the error.

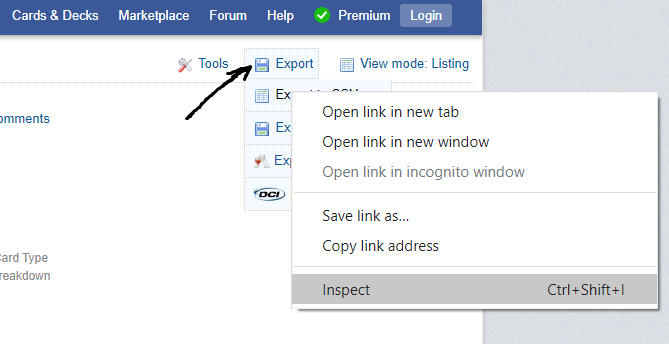
Fixing this problem is pretty straightforward, we find the xpath for the “Export” button, make sure we click on it first, and only after do we attempt to click on the “Export as CSV” button. Other threads also suggest adding a slight wait time so that the button has time to appear. Adding everything, we get:

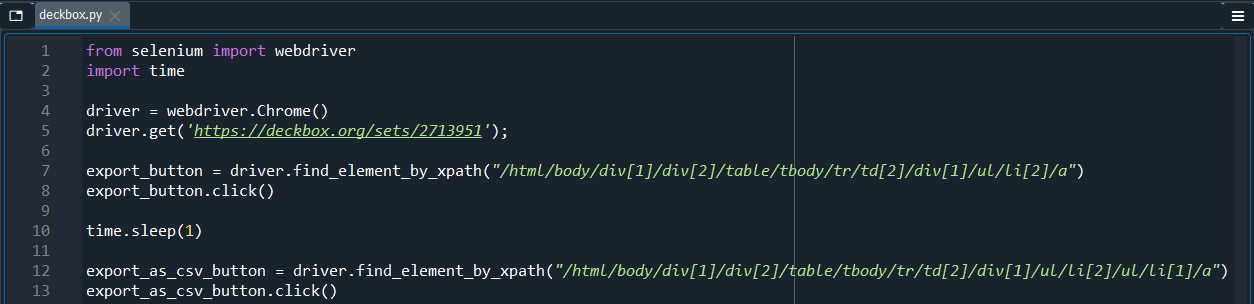
popup code

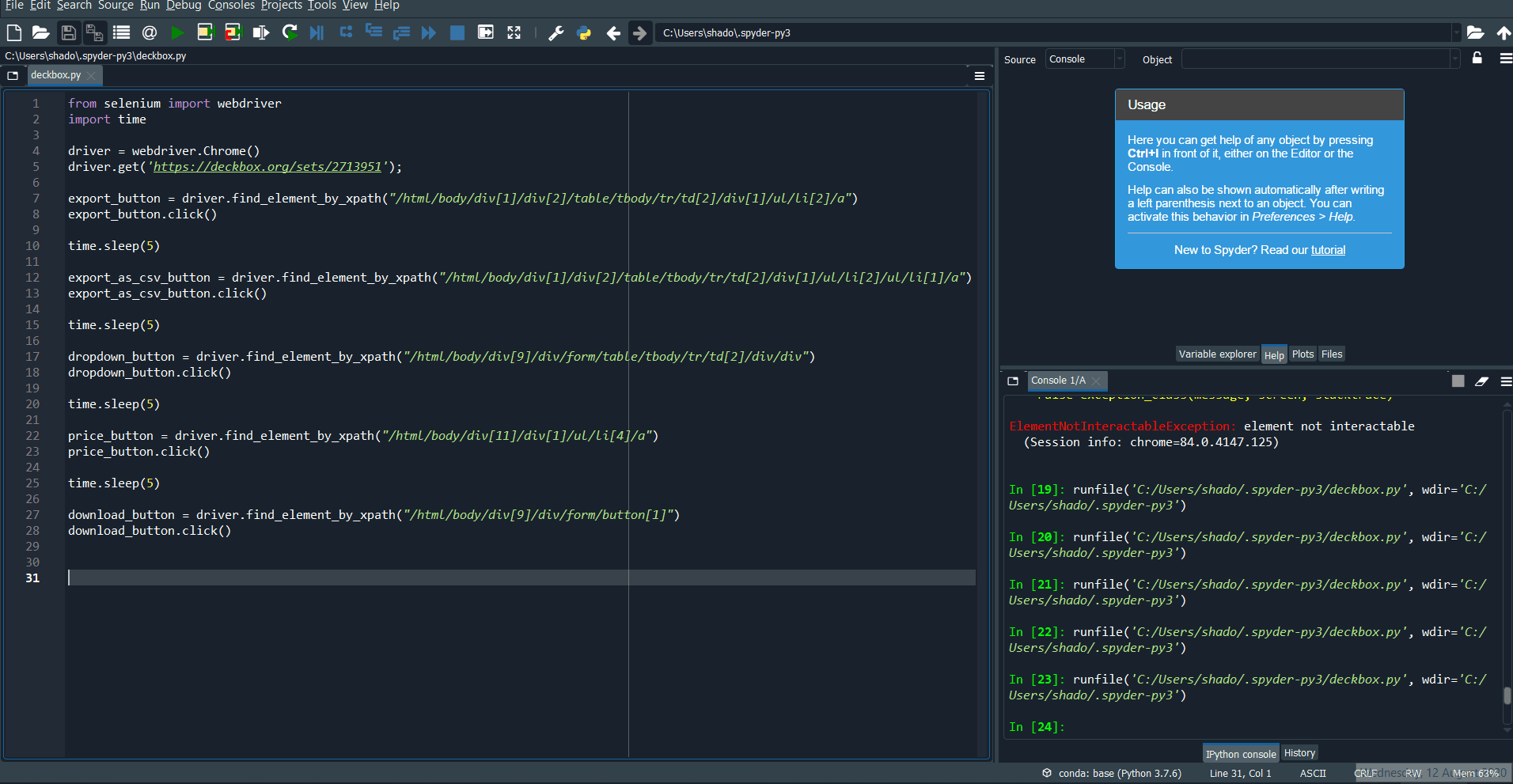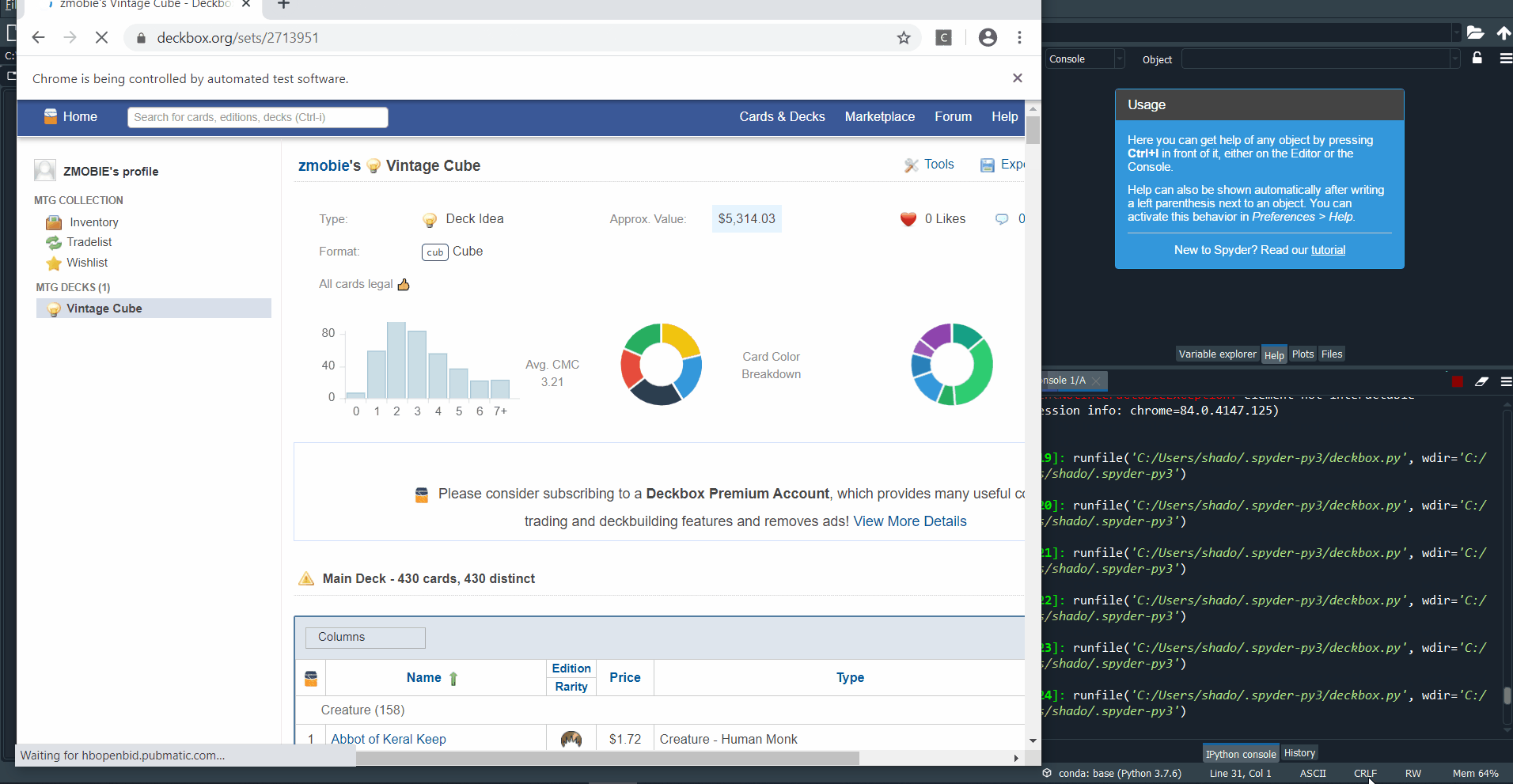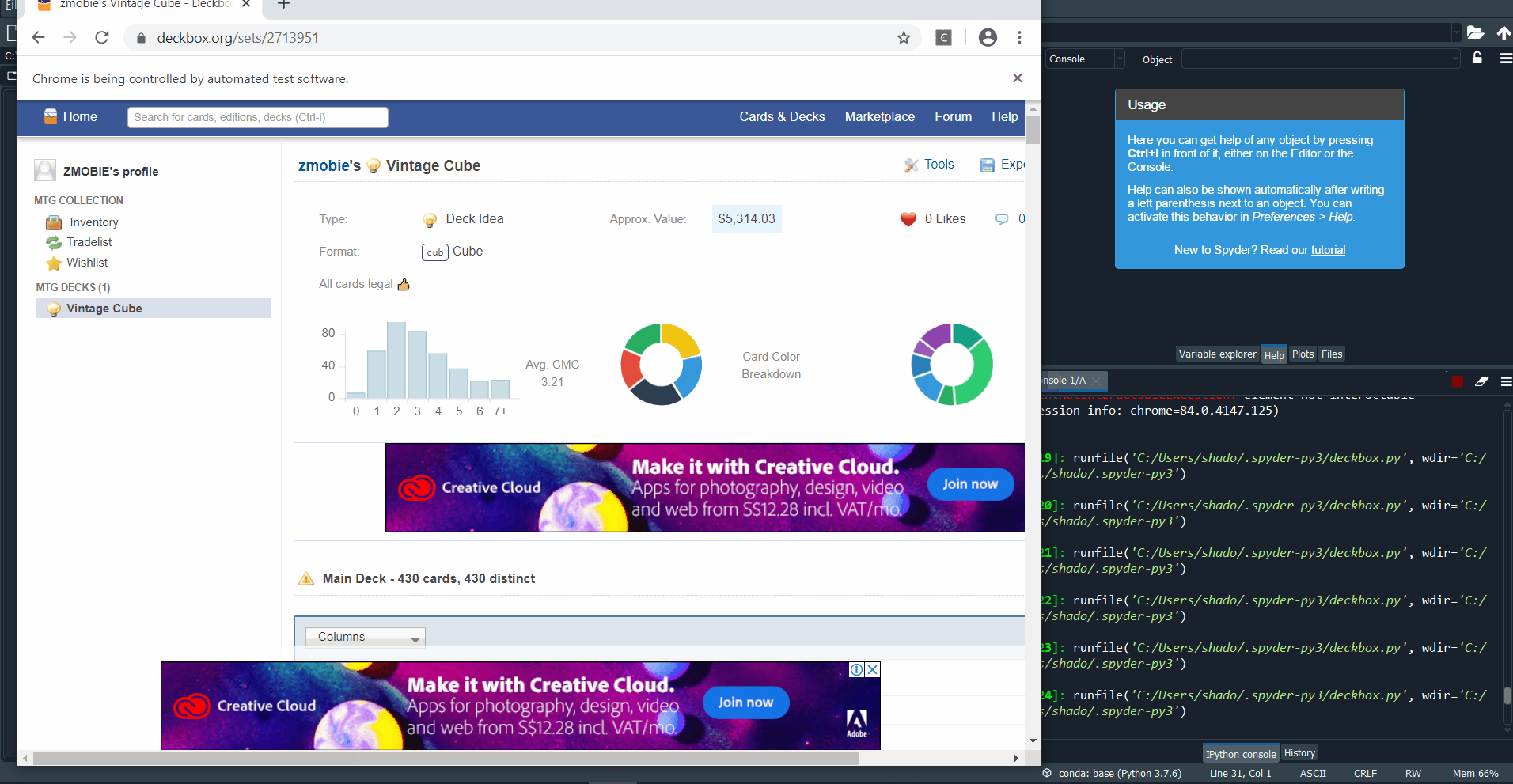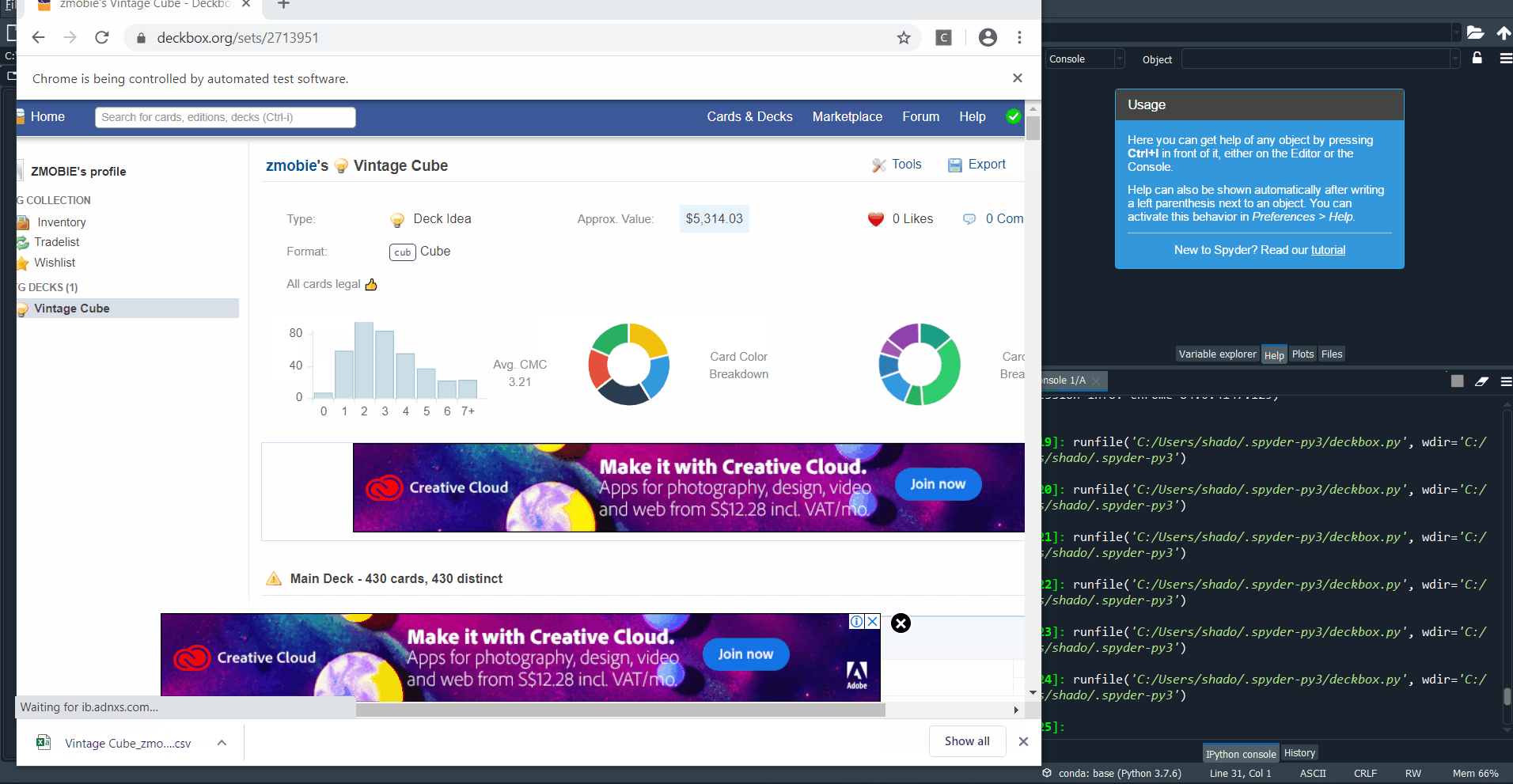
Running it yields success! The popup appears.

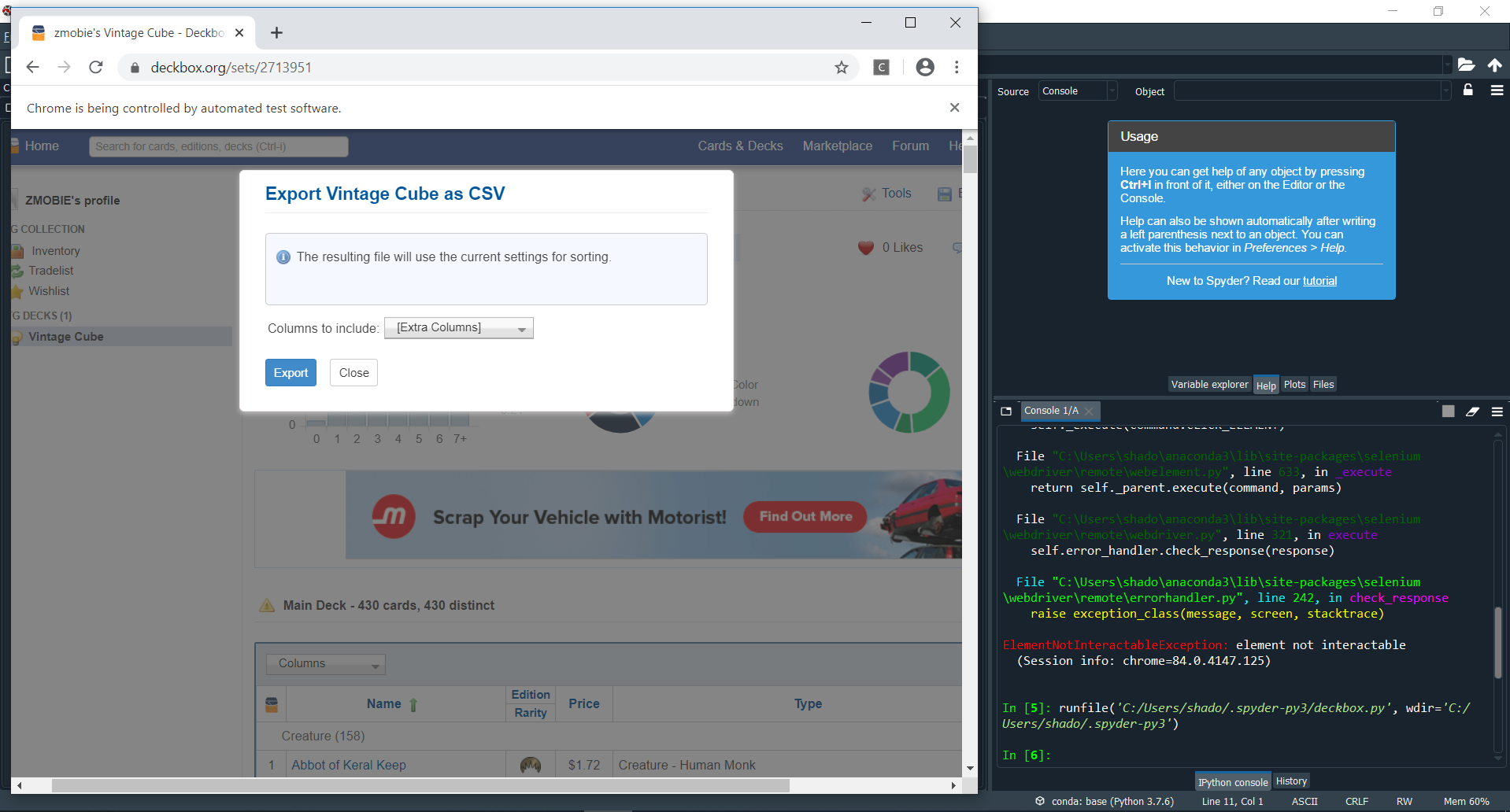
popup appears

The next step is slightly different. Instead of a button, we now have to interact with the dropdown, to add “Price” as one of the Columns to include in our requested csv. It turns out that repeating the previous steps works. We can find the xpath for the dropdown box, the “Price” entry, and then the “Export” button, and click on each of them in turn.

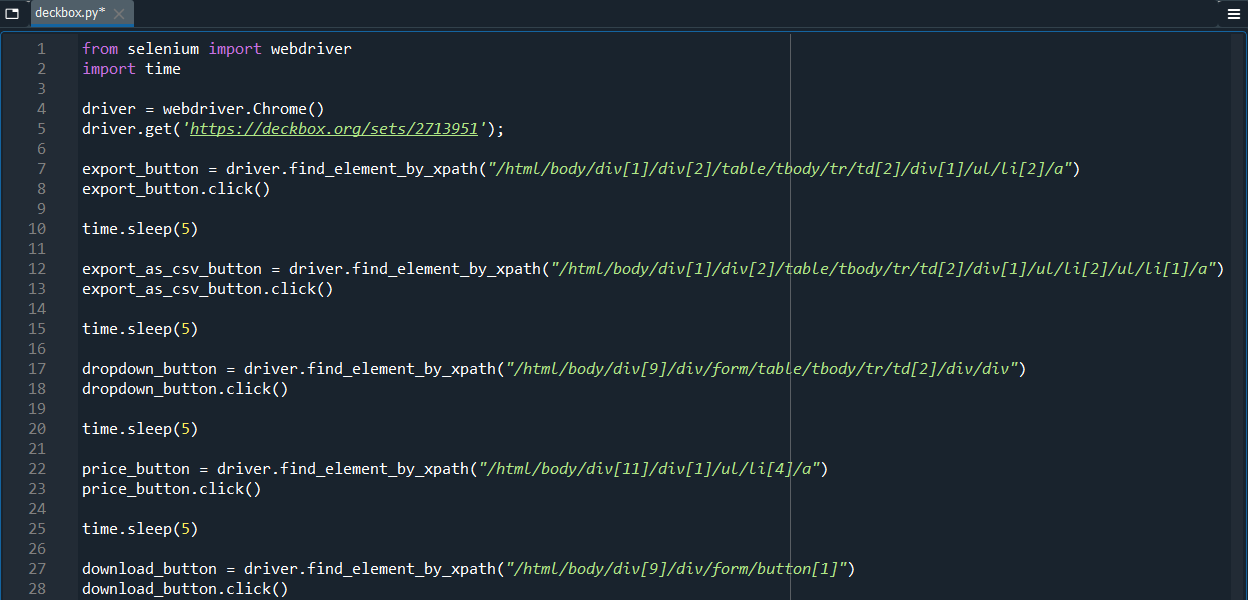
download file code

Running it, we see that it downloads the desired file into our downloads folder.

downloaded

That is one way to obtain the downloaded file. What actually happened when I originally coded it was something slightly different. When I first ran into the “element not interactable” error, I mistakenly believed that the object could not be clicked. If we take a closer look at the html for the first “Export to CSV” button that creates the popup after clicked, we see the following bit of code:

It looked like it was running some kind of code with the “onclick = ” part, so I googled “onclick = “. This brought me to this site, which explained that it was running javascript.

onclick

I next googled “selenium run javascript”, which brought me to here. Here, the syntax for executing javascript with selenium was available:

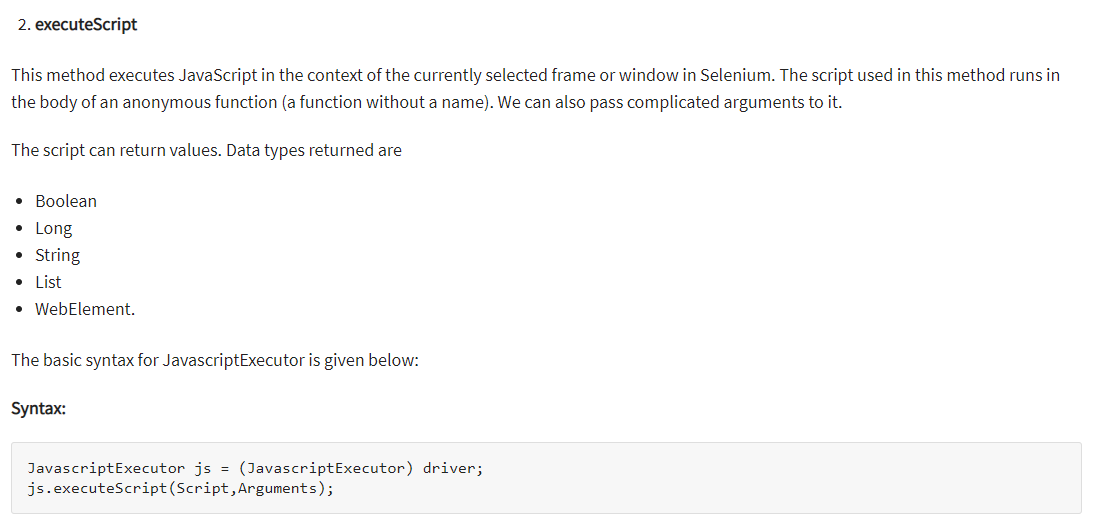
javascript selenium

A quick google of “Tcg.Set.CSVDialog” gave nothing, which made it seem like this was a custom javascript function of the website. It didn’t seem likely that I would be able to find documentation on the exact usage, so I guessed a bit. I first tried executing the first line of javascript, to see what would happen.

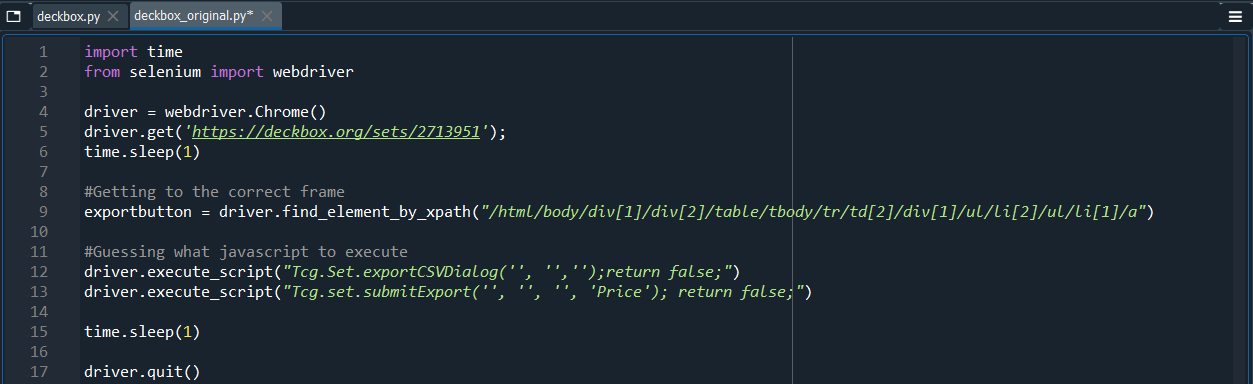
original code

The first line of javascript was successful, and opened up the popup. To obtain the second line, I went back to looking at the html for the second Export button.

final html

Again, I had to do a bit of guesswork. I wasn’t sure how I would get the “Price” Column included, but it seemed like the fourth entry of the submitExport function was the columns that had to be included in the downloaded file. I guessed that placing ‘Value’ there would work, tried it, and was greatly relieved when it did produce the desired csv file.

The coding process is oftentimes wrought with setbacks, and it is frequently not obvious how to continue with the project. A bit of luck with guessing around, or more in depth googling both help when stuck.

Updating our csv

After downloading the day’s new data, we still have to use python to append it to our old data.

csv end goal — Vintage Cube Prices.csv, running file with prices. New column to be appended with timestamp and prices.

csv generated file — Vintage Cube_zmobie_2020.August.13.csv, newly downloaded file, prices to be taken from here.

First, we have to find the downloaded csv file. Selenium puts it in our downloads folder, but deckbox has it so that the file name has today’s date too. Annoying. A quick google of “most recent file python” brings us to this thread:

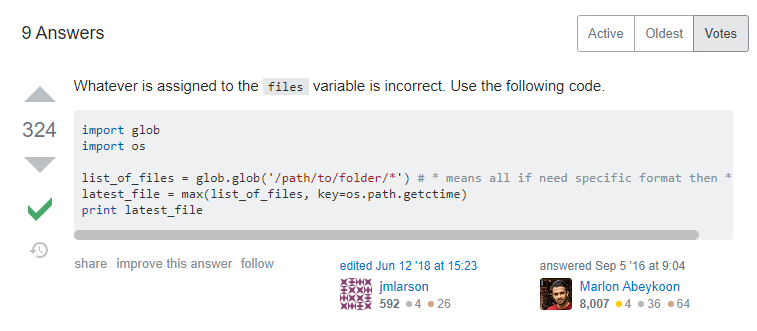
newest file

After changing the folder address to our downloads folder, we get an error:

folder error

Googling “unicode escape python error” brings us to this thread, which explains that \U is a special escape sequence in python. Huh, TIL.

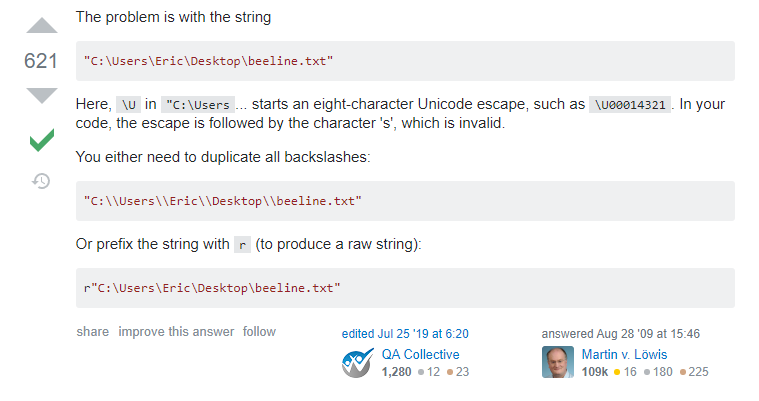
unicode escape python

Duplicating the backslashes, and running the test code, we see the latest file name as output:

python file

That’s great! This also tells us that the previous lines of code give us the full file address as output. We now have to append the Price column on this file onto our old file.

Finding resources on how to edit csvs is much easier, given how it is a much more prevalent problem. A quick look at google results of “append column csv python” brings us to this thread:

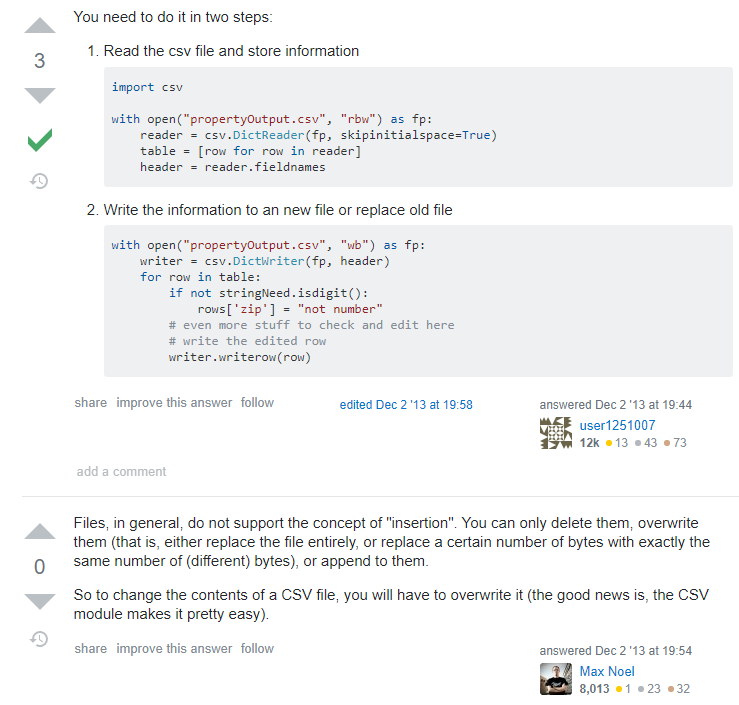
csv edit in python

explaining how reading csvs work in python. Editing current files is not supported, and we have to rewrite into a new file. Further googling yields another with code similar to what we want:

combine google

Placing our file names in, and removing the superfluous length check (Turns out our downloaded csv from deckbox has an extra 4 blank lines) gives us the following code:

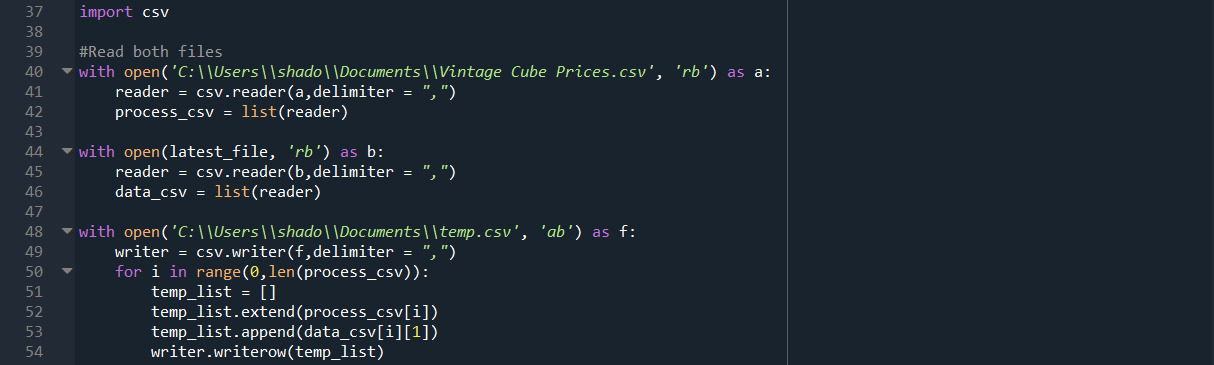
append code

Running this code, we get the following error:

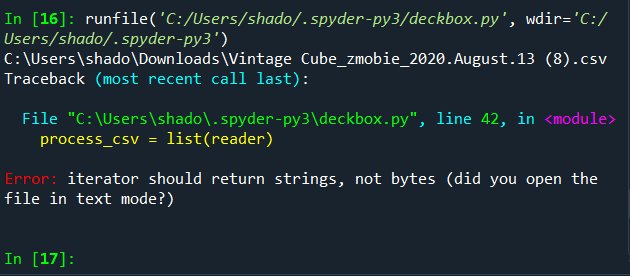
iterator error

Googling “iterator should return strings, not bytes error python”, brings us to this solution:

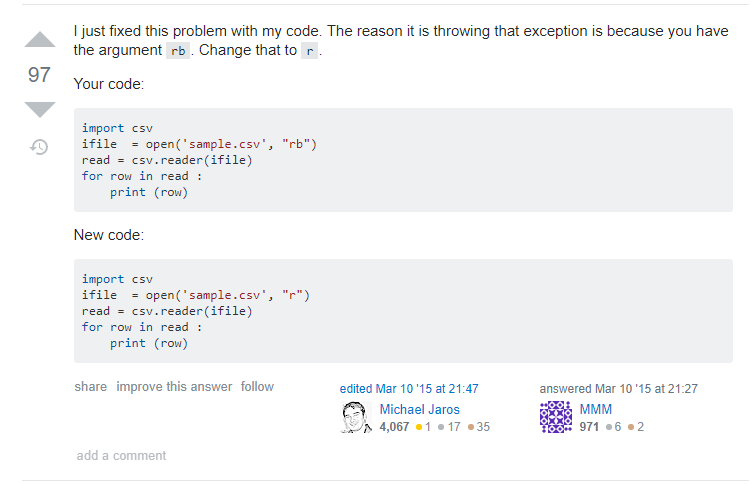
rb solution

A quick change of all the “rb”s and “ab”s to “r”s and “a”s gives us a program that runs without errors. Let’s see what our output file looks like!

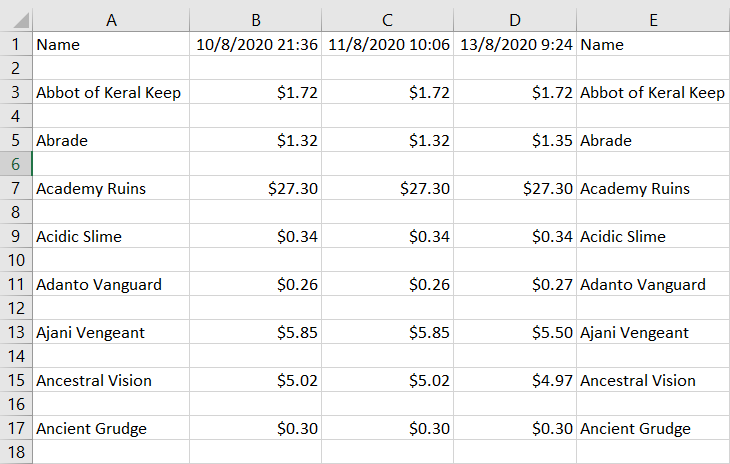
wrong output csv

Not quite right. We copied the wrong column over, we didn’t change the header row to be the current time, and there are these blank rows. Let’s fix these problems one at a time.

errorneous code

Let’s try and understand what the code is doing. At a glance, it looks like the code is iterating through each row, and creating each row by first creating an empty list “[]”, adding the original entries of “process_csv[i]”, then the “1” indexed column of “data_csv[i]”. Given that python uses 0 indexing, this corresponds to column B, explaining why the names are copied over. We should change this “1” to a “2” for column C, the price column.

For the first row, since we do not want “Price” to be copied over, we instead append the current time “datetime.datetime.now()” when i is 0.

Googling “csv blank rows python” brings us to this thread:

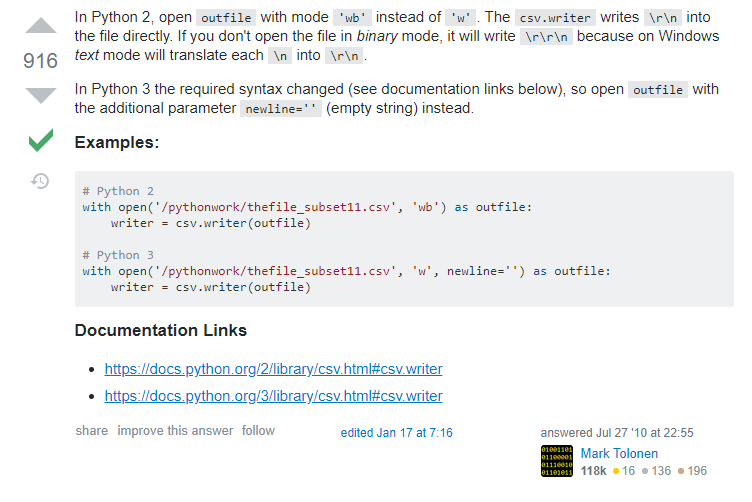
extra lines answer

Oh huh, there is some unusual interaction with the way Windows reads newline characters. Our problem is easily fixed adding the newline = ‘ ‘ parameter. Running our new code:

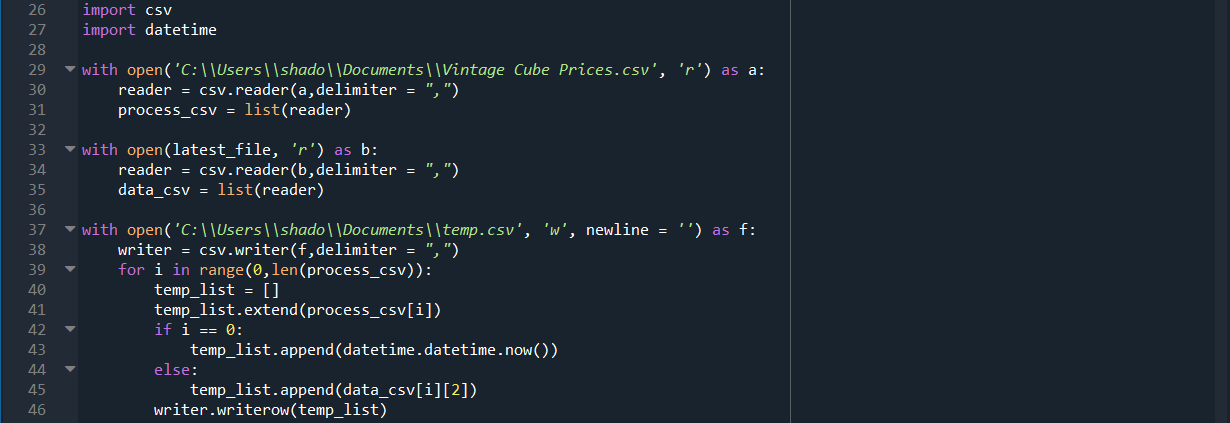
code final

Gives us our desired result, yay!

success

Our script works! For the final step, we want our script to run on startup, so lets google how to do that with “run python script on startup”. This brings us to this thread:

startup

Placing the .bat file in the folder completes our project. A quick restart of our computer verifies that the process works.

This entire post might have been too excessively detailed, but I hope it shed some light on the coding learning process. For someone inexperienced with the nuances of the language, googling things and reading things on stackoverflow is a very normal part of the process. Sometimes, when you get stuck, trying a different approach, or doing a bit of guessing goes a long way.

Zero Knowledge Proofs: Graph Isomorphism

July 24, 2019CS Problemspinkpurplepineapples

A somewhat interesting problem came up the other day, highlighting the difficulties in zero knowledge proofs. For a primer on zero knowledge proofs, an excellent reference is available here.

One of the classic examples for zero knowledge proofs is the Graph Isomorphism problem, where we ask if given $G_1$ and $G_2$ , if there is a zero knowledge proof that convinces the verifier if the two graphs are isomorphic. A description of this problem, as well as a solution to it is available in the link provided above. Reading it would provide some background for the strategies employed that follow.

Loosely speaking, a zero knowledge proof is one whose distribution of proof runs can be replicated by a probabilistic polynomial time algorithm(a simulator), one which does not have access to the oracle solver like the prover does. Recall the zero knowledge proof in the graph isomorphism case. Since permuted versions of $G_1$ all look the same, if $G_1$ and $G_2$ are isomorphic, then in the proof, sending the two permuted $G_i$ has the same distribution as sending two permuted versions of $G_1$ , which the simulator can easily provide a mapping between for. This gives some intuition as to why the previous solution works.

Problem Variant:

We now look at a slight variant of the graph isomorphism problem. Given $G, G_0, G_1$ , can we construct a zero knowledge proof to demonstrate to the verifier that one of $G_0$ or $G_1$ is isomorphic to $G$ ? In particular, to provide some intuition as to the problem here, we are trying to construct a zero knowledge proof that does not reveal to the verifier which of the two graphs is the one isomorphic to $G$ (possibly both are).

Given the previous solution, one natural strategy is to send the two graphs $\pi_0(G_0), \pi_1(G_1)$ . The verifier then sends back an integer, pointing to one of these two graphs, and the prover responds by providing the permutation from $G$ to this graph. Note that if at least one of the graphs is isomorphic to $G$ , the prover can do so with at least probability $1/2$ .

However, simulating this is a problem. Recall that in the two graph isomorphism case, since the simulator does not know anything, the simulator can only realistically send a permutation $\pi$ that it itself constructed. This means that for the simulator to simulate the prover providing the permutation from $G$ to one of the two graphs sent over, it must have been a permutation of $G$ that was sent as one of the two graphs. Hence, in the simulation, instead of sending over $\pi_0(G_0), \pi_1(G_1)$ , the simulator sends over $\pi(G), \pi_1(G_1)$ in the case where the prover picks $0$ , and the simulator sends over $\pi_0(G_0), \pi(G)$ , in the case where the prover picks $1$ . The simulator has to simulate both cases happening with probability half, for the correct distribution. However, in the event that one of the two graphs is not isomorphic to $G$ , say $G_0$ , then sending over $\pi(G), \pi_1(G_1)$ is not the same as sending over $\pi_0(G_0), \pi_1(G_1)$ , since $G$ and $G_0$ are not isomorphic, the two $\pi(G)$ and $\pi_0(G_0)$ do not have the same distribution.

This highlights two issues.

The first is that since the simulator can only realistically send back the permutation $\pi$ if $\pi(G)$ was one of the originally graphs sent, we should probably include it.
The second is that sending the graphs back without randomising the order also leaks information, since this tells us if $G_0$ or $G_1$ is isomorphic to $G$ .

We now naturally try a slightly different strategy. Instead of sending only $\pi_0(G_0), \pi_1(G_1)$ , the prover sends back $\pi(G), \pi_0(G_0), \pi_1(G_1)$ in a random order. The verifier then randomly points to one of the three graphs, and asks the prover to show that this graph is isomorphic to $G$ . The prover can do so with probability at least $2/3$ if one of the graphs is isomorphic to $G$ , and at best with probability $1/3$ if neither of the two are.

This approach also does not work. Consider what happens when we attempt to simulate this. Since we have to send $\pi$ back, in our simulation, we will have to have the prover point the graph $\pi(G)$ . However, since the simulator has to simulate the probability of failure too in the event of the verifier pointing to one of the graphs that is not isomorphic to $G$ , it has to occasionally let the verifier point to one of the other graphs. However, the simulator cannot possibly know with what probability to do so, or the graph which is non-isomorphic to $G$ which the verifier should point to. For example, if the three graphs are all isomorphic to $G$ , then the simulator should not simulate failure at all. In the event where the simulator is supposed to simulate the failure of the algorithm, the simulator too is unable to have the verifier point to the non-isomorphic graph, since it does not know which of $G_0$ or $G_1$ is the non-isomorphic graph.

This brings us a new insight.

It is a good idea for the algorithm to have a 100% success rate. More specifically, the chance of success should not differ between the cases where $G_0$ and $G_1$ are both isomorphic to $G$ , and the case where only one is.

To fix this, one natural thing to change is to have the verifier point to one of the three graphs sent over, and instead of the prover showing that this graph is isomorphic to $G$ , the prover chooses one of the other two graphs to show that it is isomorphic to $G$ . This can be done with 100% probability.

This however, can also not be simulated. Consider again what happens when the simulator tries to simulate this. The simulator cannot have the verifier point to $\pi(G)$ , since the simulator is going to send that back in the proof copy. Since the simulator does not know anything about the other two graphs, the other two graphs are essentially the same, so the best it can do is to have the verifier point to one of them randomly. This simulation does not have the right distribution over the pointed to graph. Consider the situation where one of the two graphs is not isomorphic to $G$ . In the simulated case, the graph pointed to has probability $1/2$ of being isomorphic to $G$ . In the actual proof case, the graph pointed to has probability $2/3$ of being isomorphic to $G$ .

It now becomes apparent that having the verifier point to one of the graphs is not necessarily a good idea. We now discuss a working approach (constructed by a friend). The interaction is as follows:

Verifier sends graphs $G, G_0, G_1$ to Prover
Prover responds by sending two scrambled and permuted ordered copies of to the Verifier, with an additional restriction that second scrambling of the three graphs is either a right shift, or a left shift of the original three graphs.
- In other words, it sends:
  - $\pi(H), \pi_0(H_0), \pi_1(H_1)$
  - $\pi_0'(H_0), \pi_1'(H_1), \pi'(H)$
- or:
  - $\pi(H), \pi_0(H_0), \pi_1(H_1)$
  - $\pi_1'(H_1), \pi'(H), \pi_0'(H_0)$
- where $H, H_0, H_1$ is some random permutation of $G, G_0, G_1$
The Verifier now responds with either a $0$ , or a $1$ , one option to continue with the proof, and the other to verify that the two permuted copies indeed satisfy the requirements.
If the Verifier sent a , the Prover reveals the two permutations, and we go back to step 2. If the Verifier sent a , we continue to prove that at least one of the graphs is isomorphic to , by choosing one of the columns, and showing that both of the graphs in that column are isomorphic to by sending back the permutations.
- Here by columns, we mean the graphs that are in the same position. Suppose as an example, that $H = G_0, H_0 = G, H_1 = G_1$ , that $G_0$ is the graph isomorphic to $G$ and that the Prover sent the second set left shifted(the first case above). The Prover will then in this step point to the first column, and show that both $\pi(H)$ and $\pi_0'(H_0)$ are indeed isomorphic to $G$ .

It is clear that if at least one of the two graph is isomorphic to $G$ , then the Prover can always complete step 4. To see why this approach is in fact Perfect Zero Knowledge, we construct a simulator. The simulator’s job is rather simple. To simulate the correct distribution in step 2, the simulator picks a column at random, and places two permuted copies of $G$ in those two positions. For the other two positions, the simulator permutes $G_0$ and $G_1$ , and then places them such that no column has two copies of any one graph. For example, one possible distribution would be:

$\pi(G), \pi_0(G_0), \pi_1(G_1)$
$\pi'(G), \pi_1'(G_1), \pi_0'(G_0)$

In the case where all three graphs are isomorphic, the distribution is trivially identical. In the case where only one of them is isomorphic to $G$ , notice that once we permute the graphs, this looks identical in distribution to two copies of $G$ , and one copy of some other graph $X$ . The distribution of the above simulated graphs looks precisely like some combination where neither of the two $X$ graphs are in the same column. It is easy to verify that this is indeed the case, and that the original prover verifier interaction has the exact same distribution too. For example, in the case above, if $G_0$ is isomorphic to $G$ , the above would look like:

$G, G, X$
$G, X, G$

and hence we are done. The simulator can in fact produce the same proof run with the same distribution as desired.

Characterizing Discrete Problems with Value Functions

May 17, 2018CS Problems, Mathpinkpurplepineapples

If we have a discrete problem with a solution space too large to explore, or possibly too annoying to describe, we find that oftentimes a transformation of this problem into another problem in a more continuous space is an effective strategy. We see this in combinatorial optimization, where certain types of problems, say maximum weight matching, can be transformed into a linear programming problem.

What is interesting is just how prevalent this strategy can be. Several different problems where this technique is useful will be demonstrated.

Colored, non-intersecting bipartite matching

Suppose we have a set of $n$ blue points and $n$ red points on a plane. Find a perfect matching of blue-red point pairs such that no two of the lines created by such a matching intersect. Here are two example matchings, with the one on the right being acceptable:

In the example above, we see on the left that two of the lines do indeed intersect, so it is not an accepted solution.

Is it obvious why a solution must always exist? It might be somewhat intuitive as to why it must. If we have two that are entangled as in the left picture, then we can disentangle them by switching the pairing as in the right one. The problem with this approach is that this disentanglement process may in fact create new entangled pairs. It might be possible to show that a solution always exists with this approach by adding additional criteria, but it is annoying to say the least.

What can be done is to consider the following alternative characterization of the entanglement property. Instead of finding a perfect matching such that no two lines intersect, we find a perfect matching such that the total sum of the lengths of all the lines is minimized. It is rather straightforward to see that a matching with a minimal length sum can not have any intersecting lines. If not, switching the matching as above decreases the total length. In some sense, the intuition behind what we are trying to do above manifests itself in this characterization. With this characterization, we can now solve the problem in $O(n^3)$ time with the Hungarian algorithm.

Here we digress to give the actual solution of the above problem. We can apply a divide and conquer approach by splitting the points evenly into two halves with a line partition such that each half has the same number of blue and red points. To see why this is possible, notice that for any directed line(that is not parallel to any of the $n^2$ lines between any two points), we can perform a line sweep so that the number of points on either side of this line is exactly $n$ . Here are two examples of two different lines with different angles:

We look at one fixed side of this directed line, the side counterclockwise of the arrow here, and look at the difference in the number of blue and red points. The claim is that as we make small changes to the angle of this line in which we’re doing the line sweep with, the difference in the number of blue and red points can only change by 2. If we rotate this line by 180 degrees, we see that the value of this line changes from $x$ to $-x$ , so that at some time in between, it must hit 0. There are some minor details, such as if $n$ is odd, our line sweep splits the points into sets of size $n-1$ and $n+1$ so that both sets have even number of points.

points4

To actually be able to find this line, we simply have to binary search on the angle. We note that there are only $n^2$ interesting ranges of values, which correspond to the ranges in between the angles created by the $n^2$ red-blue pairs. To mimic the angle rotation process, we binary search on this set of angles, maintaining that one endpoint has a positive red – blue count, and the other endpoint having a negative red – blue count. To find the red – blue count for any one angle, we need to do a line sweep. This can be done by considering any arbitary line $l$ with the desired angle, and finding the distances of each of the points to this line $l$ in $O(n)$ time, then using quick select to find the half of the points that belong on one side. This gives us $O(nlogn)$ time required for the divide and conquer step, and an overall time required of $O(nlog^2n)$ .

Graph Edge Colorings

Consider another problem where this approach is useful: Suppose we have a graph $G$ , with maximum degree $\Delta(G)$ . We want to look at the possible edge colorings of this graph. Suppose we know by Vizing’s theorem that an edge coloring with $\Delta(G) + 1$ colors exists. Is there an edge coloring with the number of edges of each color being precisely either $\lfloor \frac{|E|}{\Delta(G) + 1} \rfloor$ or $\lceil \frac{|E|}{\Delta(G) + 1} \rceil$ ?

Let us start with any edge coloring with $\Delta(G) + 1$ colors. Consider any two colors, call them red, and blue, and the sets of edges colored by these two colors $R$ and $B$ respectively. If we have that $|R| \geq |B| + 2$ , then we know that if we consider the subgraph generated by $R$ and $B$ , this forms disjoint cycles and paths that alternate between red and blue edges. Since there are more red edges than blue edges, there exists a component with more red edges than blue (which must be a path), and flipping the colors in this path results in a new edge coloring that has 1 more blue edge and 1 less red edge. We can see that if two colors are more than 1 apart in their edge counts, then we can bring them closer with the above approach.

With this minor lemma, it is intuitive and in fact quite straightforward to see why a coloring with each color having either $\lfloor \frac{|E|}{\Delta(G) + 1} \rfloor$ or $\lceil \frac{|E|}{\Delta(G) + 1} \rceil$ edges must exist. We simply have to consider the sets of colors with edge counts not in this range, and show that we can always bring them into the range. Consider a different way to see why this is true:

Instead of showing that a coloring exists with each color having either $\lfloor \frac{|E|}{\Delta(G) + 1} \rfloor$ or $\lceil \frac{|E|}{\Delta(G) + 1} \rceil$ edges, we look for the coloring that minimises $\sum_{i}|C_i|^2$ . Where $C_i$ is the set of edges of color $i$ . Since the sum of the $|C_i|$ is constant, this is minimised when the $|C_i|$ s are all 1 apart form each other, as desired.

Balanced Trees

It is not uncommon to see in various tree based data structures, a need to have a short tree in order to ensure logarithmic performance. We see this in union-find, where we use union by rank to ensure that our trees have logarithmic height, thus allowing the find operations to take $O(logn)$ time. We also see this in AVL trees, where maintaining the property that each node has children with heights differing by at most 1 guarantees a Fibonacci lower bound in size and hence a logarithmic bound in height.

An interesting example can be seen from this implementation of Union-Find with constant time deletions. The paper assigns a weight to each vertex of their union find tree, depending on the nature of the vertex, and then demonstrates that the total value of the tree is always large under their various operations, hence resulting in a shallow tree with logarithmic height.

Reference Paper:

Alstrup, S., Gørtz, I. L., Rauhe, T., Thorup, M., & Zwick, U. (2005). Union-Find with Constant Time Deletions. Automata, Languages and Programming Lecture Notes in Computer Science, 78-89. doi:10.1007/11523468_7

2 Card Game

October 29, 2017Uncategorizedpinkpurplepineapples

Consider this game: I write two distinct numbers on two separate cards, and allow you to pick one. You can look at the number written on the card, and you can decide if you want to switch cards. Your objective is to get the card with the higher value written on it. Is there a strategy that lets you win with >50% success?

Surprisingly, the answer is yes! Consider the following strategy: We sample randomly from any distribution $X$ , say the standard normal distribution. We compare this value $x$ with the value on the card, and change cards whenever our sampled value is higher than the value on the card.

So what’s the chance of winning with this strategy? If we let the two numbers on the two cards be $a$ and $b$ , with $a < b$ , we can consider a few cases for where our sampled $x$ ends up. If $x > b$ , then no matter which card we picked, we would switch, and the chance of success is 50%. Likewise, if $x < a$ , then we would always keep the card we picked, so the chance of success is still 50%.

If however, the value $x$ we picked happened to be between the two values $a$ and $b$ , then we would always switch to the larger card, so the chance of success is 100%. This gives us a total winning chance of $\frac{1}{2} + \frac{1}{2}Pr( a < X < b )$ .

Heavy-Light Decomposition

October 15, 2017CS Problemspinkpurplepineapples

Given a tree, suppose we assign each edge a weight, and we want to find the total cost to get from any one vertex to another. Since each path is uniquely defined, we can do either use $O(n^2)$ pre-processing to store all distances for $O(1)$ queries, or do $O(nlogn)$ pre-processing, storing the $logn$ pointers towards the root in the least common ancestor algorithm along with the distances for $O(logn)$ queries.

If we now also wish to update the edge weights, the problem becomes slightly more tricky. To support both edge weights updates and path queries, we can make use of the heavy-light decomposition.

We first notice that if we decompose the tree into disjoint chains, we can now treat the tree as this set of chains, and use various segment data structures (Like a Fenwick tree) to do point update, range queries on these disjoint chains. To get from one point to another, we simply hop from one chain to another, and use each individual segment’s range query to figure out the cost of getting from one point to the other.

For this to be quick, we require two things: we need that the number of chains any path passes through is small, and that this set of chains is easy to find.

The first claim is that we can decompose the tree into chains such that each path passes through at most $O(logn)$ chains. The decomposition into chains is as follows. For each vertex, we connect it to the child that is the larger subtree. These connections from each vertex to a child defines the decomposition into chains (and can be done in a DFS). Now, for any path from a vertex to the root, it will pass through at most $O(logn)$ chains (and this is sufficient for any path containing $O(logn)$ chains). To see why this is true, look at the path to any vertex from the root. Every time this path changes to a different chain, the size of the two nodes across this change must differ by more than 2, since the other chain is larger. Hence, there can be at most $O(logn)$ chain changes.

This is sufficient to show that there are few chain changes, so that any query will take $O(log^2 n)$ time. We also have to ensure that is it easy to find which segments we have to query. This is however relatively simple, since the path from a vertex to its least common ancestor with any other vertex passes through only from positions to ends of chains (going upwards), so determining which ranges to query is in fact easy.

This gives us the ability to complete the algorithm with complexity:

Update: $O(logn)$
Query: $O(log^2 n)$

Manacher’s Algorithm

October 8, 2017CS Problemspinkpurplepineapples

Given a string, how do you find all contiguous palindromic substrings?

A trivial search of all $O(n^2)$ strings takes $O(n^3)$ time, since we require $O(n)$ time to verify if a string is indeed a palindrome. This can be easily improved to $O(n^2)$ , by considering each position as the centre of the substring, then extending out step by step on each side to determine when it is no longer palindromic. Each possible candidate for a centre takes $O(n)$ time to verify all substrings centred around this index, and there are $O(n)$ possible indices.

Manacher’s algorithm manages to find all palindromic substrings in $O(n)$ time. Just as in the $O(n^2)$ case, we attempt to build a longest palindromic substring (LPS) array in order. $LPS[i] = k$ if the longest palindrome centred around index $i$ is of length $k$ (on each side).

The key observation to make here is the following:

If a position $i$ we are querying is contained centred at $x$ (so $LPS[x] > x - i$ ), we can take reference from $LPS[2x - i]$ to figure out what $LPS[i]$ is. There are two cases:

Case 1: If the palindrome at index $2x - i$ fits inside the large palindrome at index $x$ (so $LPS[2x - i] < LPS[x] - (x - i)$ ), then we have that $LPS[i] = LPS[2x - i]$ .
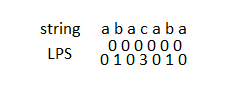
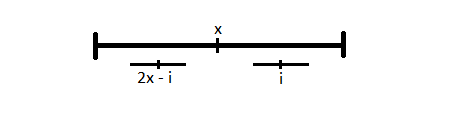Case 2: If the palindrome at index 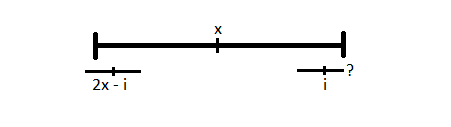$2x - i$ extends past the boundaries of the large palindrome at index $x$ (so $LPS[2x - i] < LPS[x] - (x - i)$ ), then we know that $LPS[i] >= LPS[2x - i]$ , and we will have to check what the actual value is. We now work on the LPS array in order using the above observation. We keep track of two things, the index $i$ of the current position we are trying to find the LPS of, and the furthest boundary, an $x$ such that $x + LPS[x]$ is maximal. There are $O(n)$ iterations, and each check in case 2 past the boundary extends $x + LPS[x]$ , so can only be done $O(n)$ times. This gives us an overall performance of $O(n)$ .

Articulation Point Algorithm

October 1, 2017CS Problemspinkpurplepineapples

Suppose we have a graph $G = (V,E)$ . How do we find all the vertices whose removal would cause the resulting graph to be disconnected?

Consider the following algorithm. We first take any arbitrary node of this graph, and perform a depth first search to obtain a tree. Other than the depth first search edges, we will also have the back edges pointing upwards, the edges that were not used in the depth first search.

We now have a classification for whether a vertex is an articulation point or not. For the root, the root is an articulation point iff it has two children. If it does, the two children will be disconnected upon the root’s removal. To see why this is the case, consider if two vertices were connected with a path not involving the root. These two vertices would be in the same connected component, so that a DFS would place them both under the same child.

For non-root vertices, we find that a vertex $v$ is only an articulation point if one of it’s sub-trees does not have a backward path going past $v$ .

In the above diagram, $v$ would be an articulation point if some vertex like $x$ existed, which did not have a path back up past $v$ . If all descendants of $v$ were like $y$ , and had some path back up past $v$ using edges not taken during the DFS, then $v$ would not be an articulation point.

To determine if such descendants exist, we simply have to keep track of a second variable in our DFS. Other than the depth of a node, we also keep track of the maximum height a vertex can reach with only 1 backwards going edge, and as many downwards going edges as you like. This can be done as part of the post order traversal. When each vertex no longer has any children to visit, the highest node it can get to is simply the highest any of its children can get to (which we will know since this is done post order), or the highest it itself can get to in a single upwards going step. We can then immediately tell if a vertex is an articulation point too, by looking at its children in this post order traversal. If any of its children can reach a higher vertex than $v$ , $v$ must be an articulation point. This can all be done as part of a single DFS, for $O(V+E)$ time.

Initializing an Array in O(1) Time

September 24, 2017CS Problemspinkpurplepineapples

Initializing an array usually takes $O(n)$ time, when we spend $O(n)$ time setting bits of data at a specific location in memory to $0$ . Given that our machine memory can contain junk data, how do we build a data structure(an array) that initializes in $O(1)$ time, has $O(1)$ updates, $O(1)$ queries, and $O(n)$ space (worst case analysis here). We can assume that each array entry fits in $k$ bits, and that $n$ fits in one machine word.

We use a total of three arrays to accomplish this. We do not set any of these arrays to $0$ initially. In the first array, we store our data entries, each of $k$ bits. In the second, we store the position indices of those that we have visited, in order (so that if we see an element here, we know that the element in that position in the first array is correct). At this point in time, if we also maintain a separate integer $m$ , to count the number of unique indices we have visited already, we can solve this array construction problem in $O(n)$ updates, by iterating through the second array from positions $0$ to $m-1$ , so that when we are queried, we can figure out if the element at the position index is correct by linear searching through the second array.

To avoid this problem of having to do a linear search, if we wish to figure out if position $p$ has been visited before, we store it’s position $m_p$ in a third array at position $p$ . Now, if we need to update or query the array at position $p$ , we check index $p$ in our third array, then check that value $m_p$ is less than our current second array size $m$ . If it is indeed less than $m$ , then we check if the value at the index $m_p$ in array two is indeed $p$ . If it is, we know that the value at index $p$ in the first array is correct, and we can update accordingly. If it is not inside, we can either output $0$ in the case of a query, or in the case of an update, simply increment $m$ , and update the appropriate values in the first, second, and third arrays.

Cardinality of Chains in the Power Set of the Natural Numbers

September 16, 2017Mathpinkpurplepineapples

Consider the power set of the natural numbers, $\wp (\mathbb{N})$ . If we partially order this set by inclusion, what can we say about the cardinality of these chains?

Certainly, chains of countable length exist. Consider the sets $S_{i} = \{1,2,...,i\}, i \in \mathbb{N}$ . These sets form a chain in our poset, and the chain is of countable length.

Do uncountable chains exist? Contrary to how one’s intuition might suggest that it would always be possible to go up to the next element in the chain, uncountable chains do exist. Consider any bijection from the natural numbers to the rationals, say $\phi: \mathbb{N} \rightarrow \mathbb{Q}$ . Now, consider the sets $S_{r} = \{i | \phi(i) < r, i \in \mathbb{N} \} , r \in \mathbb{R}$ . Each set $S_r$ is the set of natural numbers that maps to a rational number less than $r$ . Since this set is ordered by inclusion, and bijects to $\mathbb{R}$ , we have an uncountable chain.

What is interesting is that not all chains have the same structure. Despite being able to biject from $\mathbb{N}$ to $\mathbb{N}$ to arbitrarily permute the ordering of the elements, this ability is not sufficient for the transformation from any one chain to another.

Duplicates in an Array

September 9, 2017CS Problemspinkpurplepineapples

Problem: Consider an array of size n containing elements from $1$ to $n-1$ . We know that there must be a duplicate element. Find any such duplicate element in $O(n)$ time, and $O(1)$ additional space.

Additional challenge: Do not make any modifications to the array.

Solution